nonogram安卓版

这款安卓平台的像素解谜游戏，用简单的操作就能开启趣味挑战。它能帮助玩家锻炼逻辑思维，从学生到成年人都能轻松沉浸其中。游戏里轻松的氛围搭配舒缓的背景音乐和音效，让人玩起来就停不下来。丰富的关卡设计各有特色，每一关都能带来全新的解谜乐趣，非常值得体验。

nonogram安卓版玩法

无论是数字类还是文字类的策略游戏，操作体验都十分流畅，你对这类游戏的机制了如指掌，其独特的玩法设计总能让人沉浸其中，不知不觉就投入大量时间。

多种主题拼图等待您去挑战，不要忘了领取成就奖励

5种挑战模式，选择最适合您的数织游戏难度等级

轻松愉快的背景音乐，能使自己快速放松下来

nonogram安卓版优势

5种挑战模式，选择最适合您的数织游戏难度等级。

轻松愉快的背景音乐，能使自己快速放松下来。

这里有多种主题的拼图等着您来挑战，记得去领取完成后的成就奖励哦。

在这个充满趣味的游戏天地里，上手操作毫无门槛，日常体验轻松惬意，然而若想达到精通的境界，却需要付出大量的时间与精力去钻研。

nonogram安卓版新手攻略

本系列中的简称及其说明

排：行/列

垂直：与排的方向垂直。

在游戏场景中，若未特别说明，从k排起始的m×n区域一般涵盖所有排的整体；此外，它也可用来界定一个矩形范围，这里的m代表行数，n代表列数。

场地格：初始状态的格子，存在在游戏的区块中。

第x行格：从任意一边开始数的第x个场地格

第x个数字：从任意一边开始数第x个数字

某个数字所对应的正格，指的是那些必然存在黑色区块的场地格，并且这类场地格必定属于该数字所对应的图形构成部分。

负格：一定无黑块的格子

数字x的位：数字x所可能代表的场地格

第一章：数字的位与数字的位的确定化

1-1概述

在数织的过程中，我们始终在处理那些模糊的位置，借助这些位置与区块之间的关联，我们能够确定其中一部分的精准位置，最终顺利推演出完整的图像。

数字的具体位置通常能通过单排的格子数量与数字本身推导得出，偶尔会借助已明确的正格和负格信息，仅在极个别关卡中才需要结合两排以上的线索进行判断。这种设计让整体难度处于较为适中的水平，我们的系列内容旨在帮助新手快速成长，逐步掌握推理大多数图形的能力，成为经验丰富的玩家。

注：以下所有定理与方法中我们将把负数看为零。

1-2 推演基础

怎样借助推演来锁定精确方位？我们不妨先确立一条极为简洁的定理。

当某一行中只存在一个数字时，该行内所有非数字所在的场地格都属于负格。（1-2-1）

这条定理无需证明即可成立，也可以看作是数字位定义的另一种表述方式。

从这条公理中我们能够发现，要想明确一个数字的精确位置，关键在于把它的位数缩减到不能再缩减的程度。而交叉排列与单排列的限制条件，能够为我们缩减数字的位数提供帮助。

我们来看一个简单的例子。

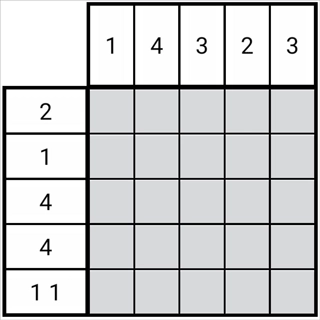
图1-2-1

如图所示，每一排的黑块依据规则仅存在有限种分布形态，这些分布形态被称作分布可能。

图里第二列存在两种不同的分布情形，这两种情形之间有重叠的区域，从这些重叠的格子能确定它们必然是正格。

同理，图中第三列存在三种可能的分布情况，而这三种分布情况之间存在一个公共区域——第三列的第三格。因此，这个格子必然也是正格。

在任意排列的所有可能分布里，始终存在黑色区块的格子被定义为正格。

当某个排中存在一个仅包含单个数字的正格时，这个正格就像一颗用于固定数字位置的“钉子”，而数字所在的位可基于此向左右两侧扩展格数，通过这种“波动”方式，便能推导出所有可能的分布情况。

当两个正格分别限定了某个数字的两端位置时，它们之间的区域必然也属于正格。这一规律也能够借助数学表述的形式重新呈现，具体如下：

若某一排中只有一个数字，并且已经明确第m行的格子和第n行的格子都是正格，那么第i行的格子也为正格。这里的i属于这样的正整数集合：i大于等于m且小于等于n，或者i大于等于n且小于等于m。(1-2-2)

然而，由于数字的大小关系，一个数字的位会在正格的两侧增加特定数量的格数。这一增加不能超出数字所规定的范围，因此我们从数学角度对其展开推导。

假设某一行中存在唯一的数字k，且已知第m行和第n行的格子均为正格（m不小于n）。根据式1-2-2，这两行之间的所有格子也都是正格，这些正格总共占据了(m - n + 1)个位置。由此可推出，该行中还能在左右两侧新增的格子数量为k减去已占据的(m - n + 1)个。因此，只需从已有的正格区域两端各增加相应数量的格子，就能得到该数字k对应的所有位置。具体来说，这些位置的范围是从第n减去新增数量的行到第m加上新增数量的行。经过整理后可以得到：

当某一排仅存在单个数字k，且第m行格与第n行格均为正格（其中m≥n）时，该数字的位置范围是从第(-k+m+1)行格延伸至第(k+n-1)行格。(1-2-2)

1-3边缘法

我们前面提到，数字可以对位形成限制，实际上，还有另一种因素也能对位产生限制，那就是场地格的边缘。场地格边缘之外显然无法存在位，特别是第一个数字，它必然离场地格的边缘最近，因此很容易受到限制。所以，我们有必要探讨边缘的相关情况。

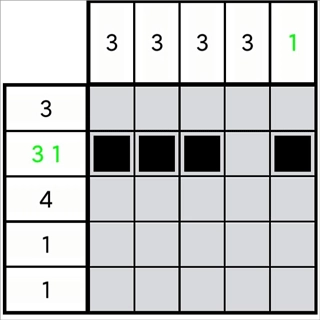
图1-3-1

如图1-3-1所示，很明显，图中第1列的位无法向上增加两格，不过它确实符合定理(1-2-3)的前置条件。我们可以换个思路：既然不能向上增加，那就必须向下增加。所以，向上不能增加的格数，向下就得相应增加多少格。

设有一排仅包含一个数字m，且已知第n行的格子为正格，其中m大于n。那么这一排中无法再增加的格子数量是(m - n)个。若将这些数量的格子向下添加，就能得出：

若某一排中存在唯一的数字m，且第n行的格子是正格，同时满足m大于n，那么对于所有属于正整数集合且处于[n，m]区间内的i，第i行的格子均为正格。(1-3-1)

观察这个定理，当m＞n时，意味着该数字对应的位必然覆盖了从第1行格到第n行格的范围。倘若我们将其假定为第一个数字，不难发现这个定理依旧是成立的。由此可得：

若某一排的第n行格是正格，且该行首个数字为m（m＞n），那么对于满足i∈[n，m]且i为正整数的所有i，第i行格均为正格。(1-3-2)

当某个数值处于边界位置时，它自身的状态不会有太明显的改变，不过，要是我们把讨论范围扩展到一整列的情况，结果又会是怎样的呢？

这里我们介绍一种方法——整体法：在确定两个相邻数字的位时，可将这两个数字视为一个整体数字来处理，它们的位也相应看作这个整体数字的位。这种处理方式能够简化运算过程，同时帮助我们分析一整排数字的情况。

我们可以留意到这样一个事实：当由多个数字构成的整体处于边缘位置时，会呈现出一种独特的分布形式——数字-空格-数字-空格。这种分布方式能将数字所占据的空间压缩到最小，我们把整体处于边缘时的这种分布状态称作边缘状态。

当一个实心物体在直线轨道上滑动时，其不同时刻的投影与初始投影的重叠区域会逐渐缩小。而物体运动过程中所有时刻投影的公共部分，与运动起止两个边缘状态下投影的公共部分是一致的。基于这一观察，我们能够推导出：

没有负格的一排中，所有可能分布的公共部分由其边缘状态所决定。

从描述来看，它表面上显得无懈可击，不过存在一处细微的不足：当多个数字作为整体时，其占据的空间能够伸缩变化，而处于边缘的状态必然是空间最紧凑的。好在目前距离将其完善仅一步之遥。

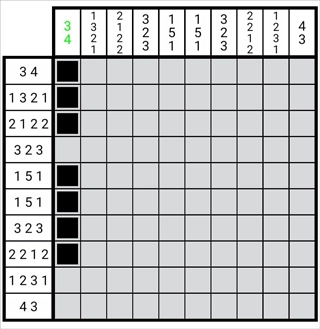
图1-3-2

我们可以在左侧第一列自上而下构建一个图形，它呈现的是该列所有数字整体的边缘形态。此时观察这一列，从下往上数存在两个空位。这表明该图形里每个数字的对应部分都能向下延伸两格，所以我们把图形中每个数字对应的部分从顶部开始向下裁剪掉两格，具体效果可参考图示。

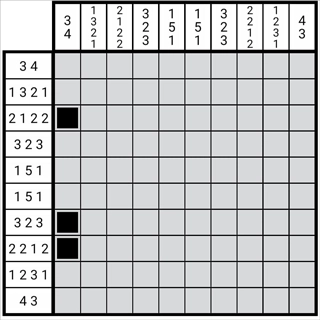
图1-3-3

这样我们便得到了这一列的正格。通过这种方法得到的最终图形，和原图形的数字位是相互对应的。此处我们省去了对边缘状态的检查——边缘状态的重叠无关紧要，关键在于重要数字与图形必须一一对应。由于这个图形能够调整长度，但其中任意一个图形的活动范围都是有限的，其限制条件恰好是自身与区块的长度。只有当图形和数字一一对应时，这种方法才具备意义。据此，我们也反向推导出了它们必然一一对应的原因，并且可以将这一性质应用到解题过程中。这也为第二章的内容做了一些铺垫。

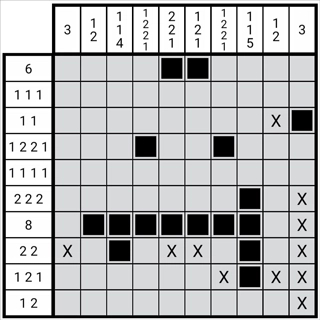
图1-3-4

如图所示，图中第七列第七行的数字2是通过该方法确定的第七列第3个数字，基于位置关系的对应性，第4个数字1的位置必然是第七列第十行。

我们可以归纳出一种快速判定正格的方法：首先按顺序从第一行格起绘制数字与空格的对应图形，接着用起始方向的数值减去剩余的空格数量（若结果为负则视为零），最终得到的图形即为正格。这类图形与原图形的位置具有对应性，也是通过第一章所有方法能获取的最多正格形式，该方法被命名为边缘法。

nonogram安卓版优势

先挑选契合自身当前能力的游戏难度，再从基础阶段一步步提升挑战等级，让游戏体验随着实力增长慢慢进阶。

通过像素化逻辑谜题挖掘更多线索，逐步揭开其中隐藏的图像。

这款纵横数字游戏上手简单，一旦开始玩就会让人特别上瘾。

舒缓的自然音效与轻柔的背景音乐交织，能迅速安抚躁动的心神，让人的内心归于宁静。

nonogram安卓版描述

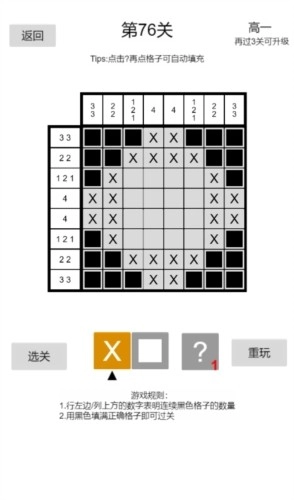
一款安卓平台的数字推理游戏，巧妙融合了逻辑解谜与艺术创作的乐趣，让玩家在数字谜题的过程中，逐步拼出精美图案，开启一段新颖独特的益智之旅。

精心设计的关卡体系：涵盖数百乃至上千个不同难度的关卡，难度梯度循序渐进，助力玩家持续突破自我。

精美的图案收集：玩家在通关后，能够解锁并收集各式各样精美的图案，以此展现自身的智慧与个性。

游戏支持免费游玩，全程打扰，让玩家能尽情享受纯粹的游戏时光。

小编点评：